Понимание статистики начинается с простого
Многие считают статистику сложной и недоступной областью знаний, особенно если они не имеют математического образования. Однако в реальности статистика — это инструмент, помогающий принимать обоснованные решения на основе данных. Объяснить сложные концепции статистики простыми словами возможно, если подходить к обучению пошагово и использовать реальные примеры из жизни. Например, когда мы смотрим прогноз погоды и видим 70% вероятность дождя — это уже результат статистического анализа. Такие повседневные кейсы позволяют сделать обучение статистике простым языком онлайн понятным даже тем, кто начинает изучать статистику с нуля.
Шаг 1. Понимание данных: описательная статистика
Начать стоит с самой базы — описательной статистики. Это раздел, который помогает упорядочить и описать данные. Среднее значение, медиана, мода — всё это инструменты, которые используются даже в социальных опросах. Например, если вы проводите опрос среди студентов о предпочитаемой форме обучения и считаете, сколько человек выбрало онлайн-курсы, а сколько очные — вы уже используете статистику. В рамках курсов статистики для начинающих объяснение таких понятий сопровождается визуализацией, что делает обучение доступным.
Шаг 2. Вероятность: интуитивное понимание неопределенности
Понятие вероятности может пугать, но его можно объяснить через знакомые ситуации. Допустим, вы вытягиваете конфету из мешка, в котором 7 шоколадных и 3 карамельных конфеты. Вероятность вытянуть шоколадную — 70%. Эта идея лежит в основе многих решений: от маркетинга до медицины. Например, врач может использовать вероятность выздоровления при выборе метода лечения. В курсах статистики для гуманитариев такие примеры помогают устранить страх перед числами.
Шаг 3. Распределения: как данные ведут себя
Типичным заблуждением является восприятие всех данных как равномерно распределённых. На практике чаще встречаются нормальные распределения — «колокол», где большинство значений сгруппированы вокруг среднего. Представьте себе рост людей: большинство находятся в пределах 160–180 см, а очень высоких и очень низких — меньше. Это классический пример нормального распределения. Репетитор по статистике для студентов часто объясняет эти концепции через графики и реальные выборки данных из соцопросов или экзаменов.
Шаг 4. Проверка гипотез: сравнение и выводы
Проверка гипотез — важный инструмент, который помогает определить, значимы ли различия между группами. Например, если вы хотите узнать, влияет ли кофе на продуктивность, вы проводите эксперимент: одна группа пьёт кофе, другая — нет. Затем вы сравниваете средние результаты. Если разница статистически значима — значит, кофе действительно влияет. Это основа доказательной медицины, психологии и даже HR-аналитики. В книге «Статистика простым языком» (которую можно купить в интернете) такие примеры подробно разбираются для лучшего понимания.
Шаг 5. Корреляция и причинность: не всё, что связано — причина
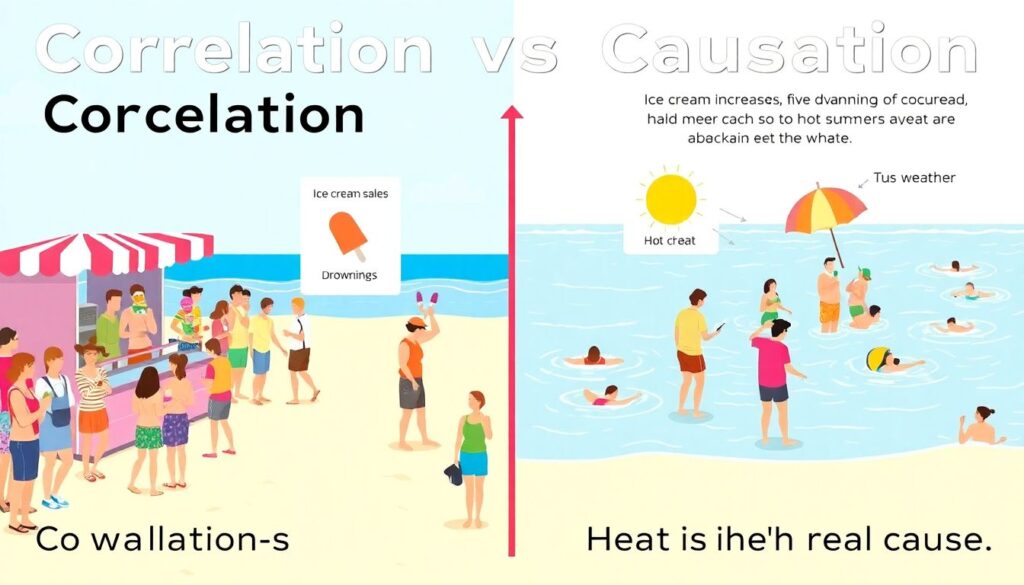
Ещё одна сложная для новичков тема — различие между корреляцией и причинностью. Допустим, данные показывают, что с увеличением количества мороженого летом растёт количество утоплений. Это не значит, что мороженое вызывает утопления. Истинная причина — жара: она увеличивает и желание есть мороженое, и количество купающихся. Объяснять такие связи легче через визуализацию и реальные данные. Многие курсы статистики для начинающих уделяют особое внимание тому, как интерпретировать связи между переменными корректно.
Распространённые ошибки и как их избежать
1. Игнорирование контекста данных. Часто новички считают, что достаточно просто рассчитать среднее значение. Однако без понимания, откуда взяты данные и что они означают, можно сделать неверные выводы.
2. Использование статистики без визуализации. Диаграммы, графики и гистограммы — незаменимы для интуитивного понимания распределения и взаимосвязей в данных.
3. Путаница между корреляцией и причинностью. Как показано выше, ошибочная интерпретация может привести к ложным выводам.
4. Недооценка вариации. Среднее значение не даёт полной картины. Два набора данных могут иметь одинаковое среднее, но сильно отличаться по разбросу значений.
Советы для новичков, изучающих статистику
1. Начинайте с практики. Используйте реальные данные — например, из открытых источников, чтобы попробовать применить базовые методы на практике.
2. Ищите объяснения на доступном языке. Книга «Статистика простым языком» (её можно купить в онлайн-магазинах) — отличный пример того, как сложные концепции превращаются в понятные шаги.
3. Занимайтесь регулярно. Онлайн-обучение позволяет двигаться в удобном темпе, но важно не делать большие перерывы.
4. Работайте с наставником. Репетитор по статистике для студентов поможет разобраться в трудных моментах и даст обратную связь по практическим заданиям.
Заключение: статистика — это навык мышления
Понимание статистики — это не просто знание формул, а способность мыслить критически, анализировать данные и делать обоснованные выводы. Сложные концепции становятся доступными, если объяснять их через знакомые ситуации, использовать визуальные образы и избегать распространённых ошибок. Независимо от уровня подготовки — будь то гуманитарий, студент или профессионал — статистика с нуля для гуманитариев или курсы статистики для начинающих помогут освоить этот важный навык. Главное — не бояться начать.

